低次元量子流体の研究
量子流体とは?
普通の物質は,冷却すると液体から固体になります.
しかし,量子性が強く,絶対零度まで液体として存在するものを量子流体と
呼んでおり,物質の中で唯一絶対零度までこおらない液体ヘリウムは,代表的な量子流体です。
このように量子性の強い量子流体では,本来微視的な領域で顕著に現れる量子効果が,我々は眼で
見ることができるような巨視的なスケールで起こる現象を引き起こします.
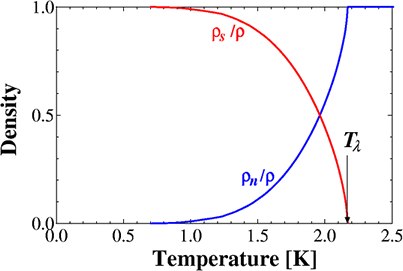
(ρn)の温度変化
1次元ナノ細孔中液体4Heの超流動
低次元化,特に1次元極限の実現へ向けて
ここで言う低次元化というのは,ヘリウム原子の動ける方向の 自由度が制限されることを意味します.2次元系であれば,高さ方向の運動が制限され, 平面内のみを動くことができます.そのような系では超流動を引き起こす原因とされていた ボーズアインシュタイン凝縮(BEC)が起こらないため,当初,超流動転移はないだろうと 考えられてきました.ところが,1973年,J. M. KosterlitzとD. J. Thoulessが渦対生成という特殊な機構に より,2次元系でも超流動転移が起こることを予言しました. その5年後,実際にヘリウム薄膜(2次元系)で超流動転移が観測されました. (Kosterlitz氏とThouless氏は2016年に,この業績によってノーベル物理学賞を受賞しています.) さらに次元を下げて,1次元系にしたとき,超流動は現れるのでしょうか. 私たちは,その答えを見つけるために,非常に細い細孔に4Heを閉じ込めることで,断面内の運動が制限された(擬) 1次元系の実現を目指してきました.
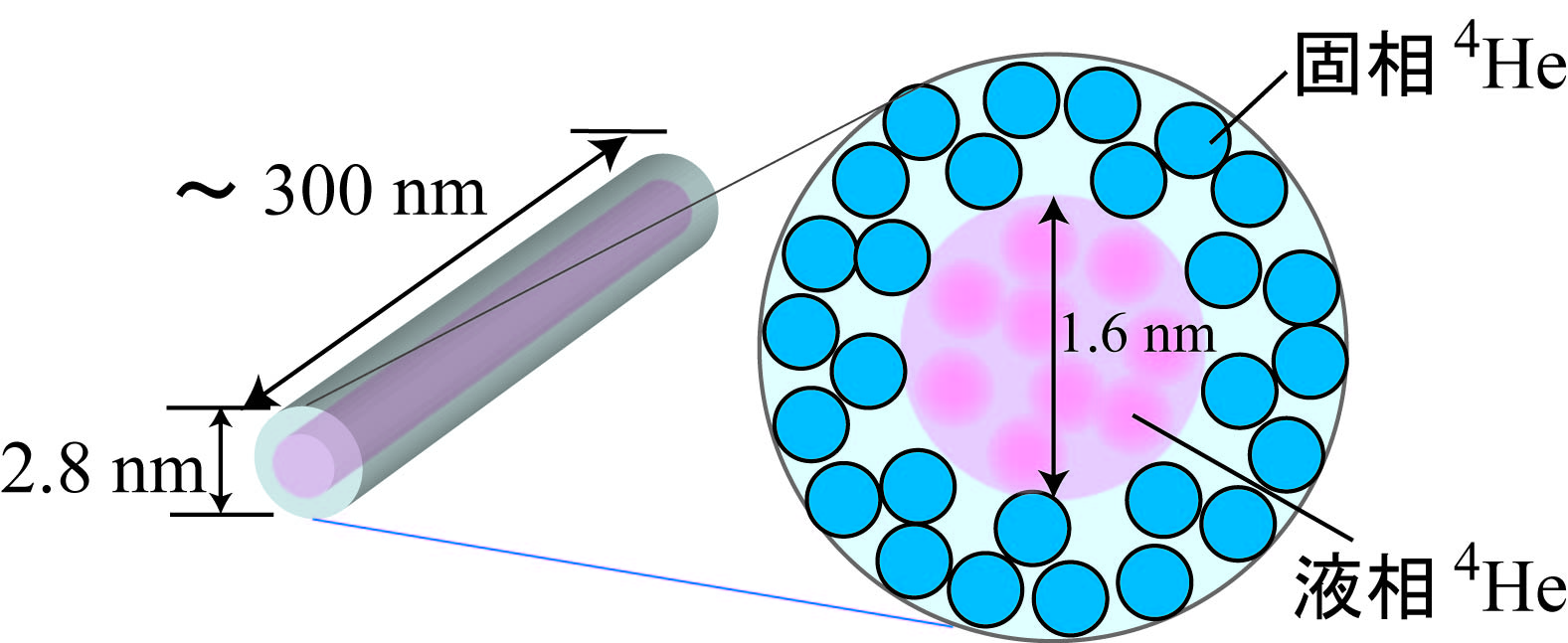
孔径2.8 nm細孔中液体への超流動応答
ここでは,実際に孔径2.8 nmのナノ細孔(図2)に4Heを閉じ込め,その超流動性をねじれ振り子法により実験的に 調べた結果を紹介します.ねじれ振り子は,ねじれロッドと試料セル(細孔と4Heが中にある)で構成され, 超流動成分を共振周波数の上昇として検出するものです.孔径2.8 nmの細孔中では,超流動はバルク4Heの 転移温度より1 K以上低温で観測されました.つまり,バルクに比べて非常に強く抑制されてはいるものの, 超流動応答が起こることが分かったのです[1].また,バルクの場合とは異なり,超流動の成長がエネルギー散逸の ピークを伴うことも明らかになりました.
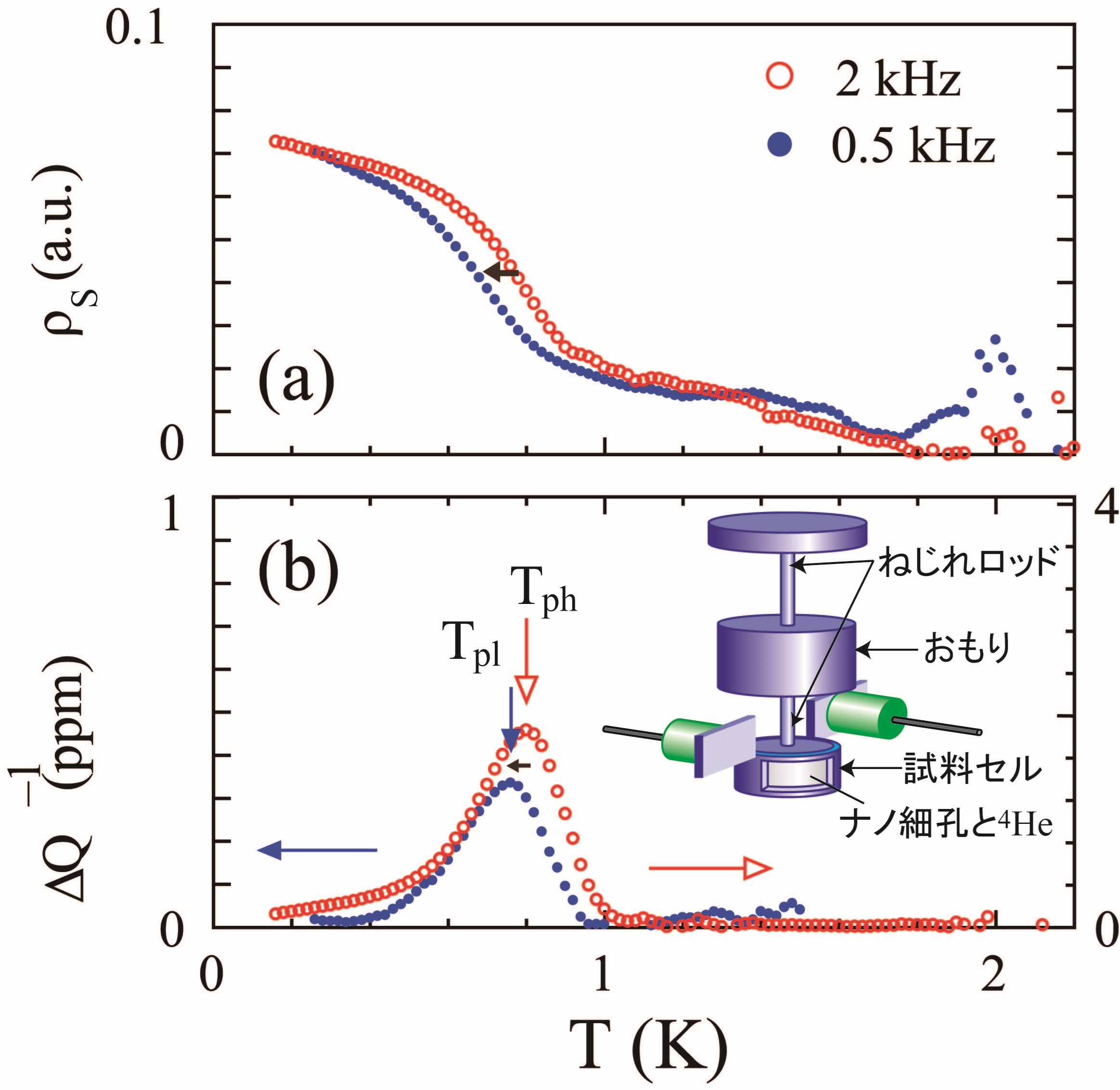
応答.Tph, Tplはそれぞれ2,0.5 kHzに
おける散逸ピーク温度. 挿入図は2重連成
振り子の模式図.
私たちはこの散逸ピークに注目しました.散逸ピークが超流動の成長がもっとも急になる温度に現われる という形は何らかの緩和現象に由来していることを示唆しています.緩和現象であれば,観測周波数によって 散逸ピーク温度の移動が見られるはずです.そこで,私たちは複数の周波数で超流動を観測することを考えました.そのために,ねじれロッドに試料セルと錘をつけることで二つの 共振モード(2 kHzと0.5 kHz)を持たせた,2重連成振り子を開発しました.その結果,図3に示すように,超流動の 急な成長が,観測周波数を2 kHzから0.5 kHzに下げることで40 mK程度低温にシフトしていることが分かりました.[2]同時に 散逸ピーク温度も同程度低温側にシフトしました.
この観測事実に対し,Eggelらは,1次元系を記述する朝永-ラッティンジャー(TL)液体モデルを用いて, 容器(ナノ細孔)の運動に対するヘリウムの応答を計算し,この大きな周波数依存を再現しました.[3]さらに, この周波数依存の圧力依存も判定量的に説明され,観測された特徴が1次元系特有のものであることが分かりました. 1次元超流動の探索は2000年ごろから行われてきたのですが,ここに来てようやく,その特徴の一端を 捉えることができたのです.
[1] J. Taniguchi, Y. Aoki, and M. Suzuki, Phys. Rev. B 82, 104509 (2010).
[2] J. Taniguchi, K. Demura, M. Suzuki, Phys. Rev. B 88, 014502 (2013).
[3] T. Eggel, M. A. Cazalilla, M. Oshikawa, Phys. Rev. Lett. 107, 275302 (2011).
現在進行中の研究課題
MEMSを用いたナノ共振器の開発

上記のように,1次元細孔内4Heの超流動が大きな周波数依存を持つことが明らかにできましたが, まだその詳細は明らかになっていません.特に,Eggelらの理論計算では,散逸ピーク温度が観測周波数に対し べき的な依存性を持つことが予測されています.そこで,より広範囲に周波数依存を調べることを次の目標と しています.従来用いられてきたねじれ振り子で安定した共振が得られるのは,kHz帯に限定されてしまうため, 新しい測定手法を開発中です.その一つが,アルバータ大学Davisグループと共同で開発しているナノヘルムホルツ 共鳴器です.(図4参照)
ヘルムホルツ共鳴は,ガラス瓶に水を入れて口のところを吹くと音が出る現象でよく知られています.その音(共鳴周波数)は, 水を増やして,ビンの中(キャビティ)の体積を減らすことで,高くすることができます.キャビティの中に液体4He を入れた場合,キャビティの高さや口の大きさを粘性進入長より小さい数100nmで作ると,超流動が現われたときのみ共鳴 が起こります.また,常流動成分の振動によるロスがないため,共振のQ値(超流動の測定感度)を高くすることができます. 私たちは,MEMSを用いて,ナノスケールでキャビティのサイズを制御することで,より広範囲の共振周波数を実現しようと しています. 将来的には,このナノヘルムホルツ共鳴器に1次元ナノ細孔を組み込むことで,1次元超流動の観測周波数依存に関する研究を 進めていきたいと考えています.加圧によって引き起こされる超流動量子相転移
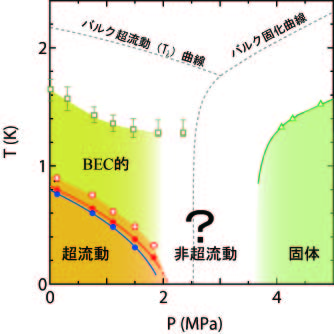
-圧力相図
現在,低次元系の分野で精力的に研究が勧められている現象の一つに,量子相転移とその相転移における 量子臨界現象があります.一般に物質は,温度を変化させると(例えば,水が氷になるように)相転移を起こします. このような相転移は熱揺らぎの効果で起きるものです.それでは,熱揺らぎのない絶対零度近傍では,相転移は 起こらないのでしょうか.実際には,量子揺らぎが存在するために,磁場や圧力を変化させると様々な相転移(量子相転移)が起こります. このような転移点の近傍では,強い量子揺らぎのため,新しい基底状態や低エネルギー励起状態が 出現することが期待され,それらを量子臨界現象と呼んでいます.これまで量子臨界現象は, 主に磁性体を対象として研究が進められてきました.
私たちは,量子効果の強いヘリウムにおいても,加圧により新奇な量子臨界現象が起こるのではないかと 期待しています.図5は,これまでに明らかになった孔径2.8 nm細孔中4Heの温度-圧力相図です.バルクの 4Heの場合,加圧すると基底状態は,液体(超流動)から固体へと転移します.しかし,ナノ細孔内では, 超流動層から“非超流動液体”相を経て固相への量子相転移が起こることが分かってきました.ボーズ液体4He の基底状態が非超流動相となるというのは非常に不思議な現象で,低(1)次元系特有の強い量子揺らぎに起因している ことが考えられます.この非超流動相が何なのかを明らかにするために,比熱・超音波測定などを進めています.
吸着膜の界面摩擦の研究
簡単な背景
ナノトライボロジーは,これまで物理学において未到達の分野でした.機械の微細化が 急速に進む中,摩擦のため素子が動かないという状況が多発し,産業からの要請として, 原子レベルで摩擦を制御するために必要な知見が必要となり,このような分野が生まれました. 一方で,基礎研究の立場からは,制御するにはまず原子レベルで摩擦の機構を解明する必要が あるということで,ナノトライボロジー分野の研究が始まりました.私は、これまで 蓄積してきた吸着膜に関する実験技術(水晶マイクロバランスや超音波測定)を活かし, 物理吸着膜と基板の間の界面摩擦について研究しています.
物理吸着膜の摩擦は,膜構造に強く依存すると考えられています.この物理吸着膜の摩擦の研究に 水晶マイクロバランス法を用い,膜構造との関係を初めて観測したのは,Krimらのグループでした. 最初に摩擦が測定された系は金基板上Kr吸着膜で,吸着膜の面密度を上げていくと,液相から固相 になる面密度で摩擦の増加が観測されました. この結果は,(液体の方がよく滑りそうだという)直感に反し,大変注目されました. 数年後,ロビンスらのグループが,膜が変形して,基板の周期ポテンシャルの 底にはまる原子が多いほど,摩擦が大きくなることを解析的に示しました.つまり,変形しやすい流体相のほうが 摩擦が大きくなるというわけです.
メゾポーラスシリカ上4He吸着膜の摩擦
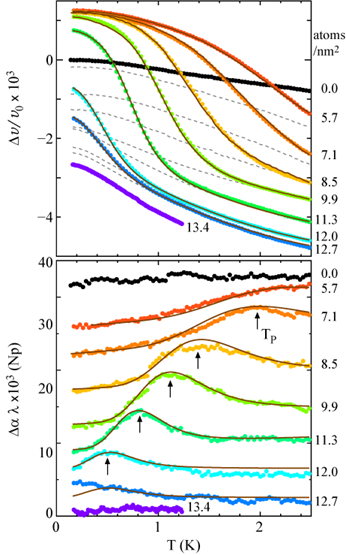
における,音速および吸収の温度変化.
Kr吸着膜の研究では,温度一定のもと,面密度を変えることによって、 膜構造を変化させていましたが,膜構造は温度によっても変化するはずです.我々は, メゾポーラスシリカ上He吸着膜に対して,面密度・温度を変えながら超音波測定を行いました.
左図は上が音速,下が吸収の温度変化を示しています.音速は温度の増加とともに,吸収の ピークを伴いながら,緩やかに減少しています.この温度による音速変化の大きさは,単原子層領域では, 吸着ヘリウム全てが基板の振動からデカップルした時の変化量に相当します.さらに面密度を増加させると, この音速の変化は小さくなり,超流動が現われる面密度nCの低面密度側で消失します.つまり, nCで吸着膜は完全に基板に固着します.
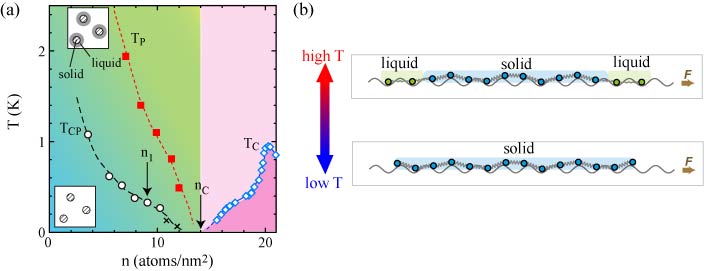
低温で吸着膜が滑る現象と膜構造との関係を明らかにするために,比熱や捩れ振り子によって 分かっている相図を示します(図7(a)).比熱のピーク温度TCPより十分低温では, 固体の島ができていて,TCPより十分高温になると,その周りに流体相が出現します. 吸着量を増やしていくと,流体相への活性化エネルギーは小さくなっていき,より低温で 流体が現れるようになります.そして,nCで不活性相が完成し,その上に,液相が形成され, 低温で超流動が現れます.
比熱から得られた相図に、超音波で観測された吸収ピーク温度TPをマスでカップリングが起きる 典型的な温度としてプロットしてみると,比熱のピーク温度の4倍程度のところに あることがわかります。さらに,比熱のピークが観測される吸着量領域と吸収ピーク温度のそれが よく一致していることがわかります.これらのことから,流体相への励起が十分起こると, 膜全体が基板に追随するようになると考えられます.
このような振る舞いは,定性的には,ロビンスらが主張したように,流体相の変形のしやすさのために, 基板ポテンシャルに固着しやすくなったと考えると理解できます.図7(b)に示すように,固体の島のみが存在している場合, 基板を動かすと,一部の原子はより高いポテンシャルに,そして一部の原子はより低いポテンシャルの位置に動きます. 結局,これらのエネルギーの損得が相殺され,固体の島は容易に基板の振動からデカップルすることができてしまいます. 一方,固体の島の周りに流体相ができると,この流体相が基板の周期ポテンシャルの底にロックされていることにより, 島全体も基板に追随すると考えられます.
このように,面密度だけでなく,温度による膜構造変化も摩擦の大きな変化を引き起こすことが 実験的に明らかになりました.膜構造だけでなく,超伝導転移のような基板の物性の変化によっても摩擦が変化しうる, ということが指摘されており,吸着膜の摩擦において,温度というパラメータが摩擦の制御においてますます 重要になってくるのではないかと考えています.